Câu hỏi
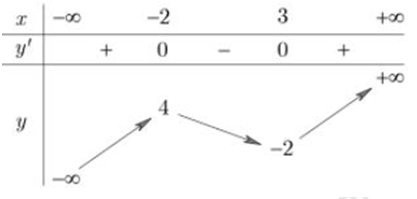
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ bên. Số nghiệm của phương trình \(\left| f\left( x-1 \right) \right|=2\) là:
- A 5
- B 4
- C 2
- D 3
Phương pháp giải:
Cách 1:
+) Dựa vào bảng biến thiên suy ra hàm số \(y=f\left( x \right)\) từ đó suy ra hàm số \(y=f\left( x-1 \right)\) và đồ thị hàm số \(y=\left| f\left( x-1 \right) \right|.\)
+) Số nghiệm của pt \(\left| f\left( x-1 \right) \right|=2\) là số giao điểm của đồ thị hàm số \(y=\left| f\left( x-1 \right) \right|\) và đường thẳng \(y=2.\)
Cách 2:
+) Để có đồ thị hàm số \(y=f\left( x-1 \right)\) ta tịnh tiến đồ thị hàm số \(y=f\left( x \right)\) sang phải 1 đơn vị.
+) Lập bảng biến thiên của hàm số \(y=f\left( x-1 \right)\) từ đó suy ra dáng điệu đồ thị hàm số \(y=\left| f\left( x-1 \right) \right|\) và biện luận số nghiệm của phương trình \(\left| f\left( x-1 \right) \right|=2.\)
Lời giải chi tiết:
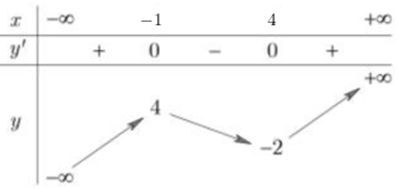
Dựa vào BBT của đồ thị hàm số \(y=f\left( x \right)\) ta suy ra BBT của đồ thị hàm số \(y=f\left( x-1 \right)\) bằng cách tịnh tiến đồ thị hàm số \(y=f\left( x \right)\) theo vector \(\overrightarrow{v}=\left( 1;0 \right)\).
BBT đồ thị hàm số \(y=f\left( x-1 \right)\):
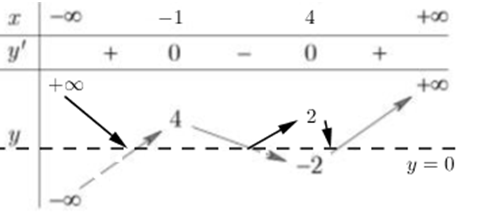
Từ đó ta suy ra đồ thị hàm số \(y=\left| f\left( x-1 \right) \right|\) có BBT như sau:
Số nghiệm của phương trình \(\left| f\left( x-1 \right) \right|=2\) là số giao điểm của đồ thị hàm số \(y=\left| f\left( x-1 \right) \right|\) và đường thẳng \(y=2\).
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y=2\) cắt đồ thị hàm số \(y=\left| f\left( x-1 \right) \right|\) tại 5 điểm phân biệt, do đó phương trình \(\left| f\left( x-1 \right) \right|=2\) có 5 nghiệm phân biệt.
Chọn A. .