Phương pháp giải:

Xét hàm số \(y={{x}^{2}}-2x+m=f(x)\).

Chia các trường hợp của m để tìm GTLN của hàm số \(y=\left| {{x}^{2}}-2x+m \right|\)

Lời giải chi tiết:

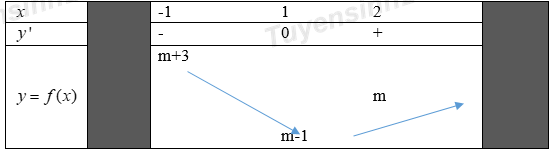
Xét hàm số \(y={{x}^{2}}-2x+m=f(x)\) có :

\(y'=2x-2=0\Leftrightarrow x=1\)

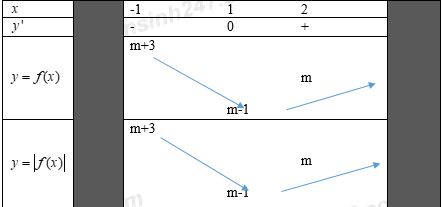
Bảng biến thiên:

+) \(m\ge 1\) :

\(\underset{\left[ -1;2 \right]}{\mathop{Max}}\,\left( \left| {{x}^{2}}-2x+m \right| \right)=f(-1)=m+3=5\Rightarrow m=2\,\) (Thỏa mãn)

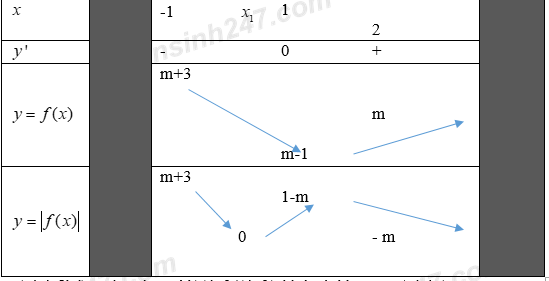
+) \(0\le m<1\):            

\(\underset{\left[ -1;2 \right]}{\mathop{Max}}\,\left( \left| {{x}^{2}}-2x+m \right| \right)=\underset{{}}{\mathop{Max}}\,\left\{ m+3;1-m \right\}=5\)

Ta có: \(m+3-(1-m)=2+2m>0,\forall m\in \left[ 0;1 \right)\Rightarrow \underset{{}}{\mathop{Max}}\,\left\{ m+3;1-m \right\}=m+3=5\Rightarrow m=2\) (Loại)

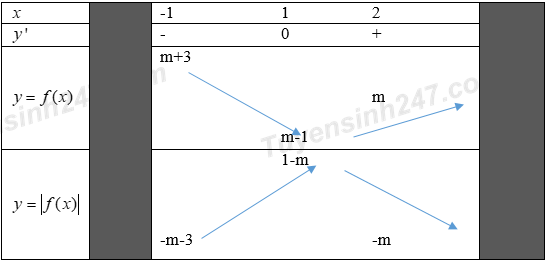
+)  \(-3\le m<0\):

\(\underset{\left[ -1;2 \right]}{\mathop{Max}}\,\left( \left| {{x}^{2}}-2x+m \right| \right)=\underset{{}}{\mathop{Max}}\,\left\{ m+3;1-m \right\}\)

Ta có:

\(m+3-(1-m)=2+2m=0\Rightarrow m=-1\in \left[ -3;0 \right)\)

Nếu \(-3\le m\le -1\) thì  \(\underset{{}}{\mathop{Max}}\,\left\{ m+3;1-m \right\}=1-m=5\Rightarrow m=-4\) (Loại)

Nếu \(-1<m<0\) thì  \(\underset{{}}{\mathop{Max}}\,\left\{ m+3;1-m \right\}=m+3=5\Rightarrow m=2\) (Loại)

+) \(m<-3\) :

\(\underset{\left[ -1;2 \right]}{\mathop{Max}}\,\left( \left| {{x}^{2}}-2x+m \right| \right)=1-m=5\Rightarrow m=-4\) (Thỏa mãn)

Vậy \(m\in \left\{ -4;2 \right\}\Rightarrow m\in \left( -5;-2 \right)\cup \left( 0;3 \right)\).

Chọn: A