Phương pháp giải:

Xét hàm số \(g\left( x \right)={{x}^{3}}-3{{x}^{2}}\) .

Sử dụng điều kiện để \(f\left( a \right);f\left( b \right);f\left( c \right)\) là ba cạnh của tam giác (BĐT tam giác).

Dựa vào GTLN và GTNN của hàm số \(g\left( x \right)\) để tìm điều kiện của m.

Lời giải chi tiết:

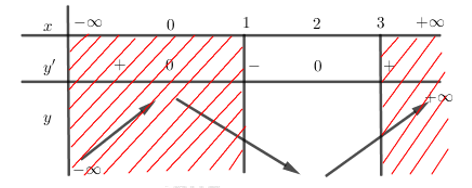
Đặt \(g\left( x \right)={{x}^{3}}-3{{x}^{2}}\) ta có \(g'\left( x \right)=3{{x}^{2}}-6x=0\Leftrightarrow \left[ \begin{align}  x=0 \\  x=2 \\ \end{align} \right.\)

BBT :

\(\Rightarrow \underset{\left[ 1;3 \right]}{\mathop{\min }}\,g\left( x \right)=g\left( 2 \right)=-4;\,\,\underset{\left[ 1;3 \right]}{\mathop{\max }}\,g\left( x \right)=g\left( 3 \right)=0\)

\(\Rightarrow \underset{\left[ 0;2 \right]}{\mathop{\min }}\,f\left( x \right)=-4+m\)

Với mọi a, b, c ta có \(f\left( a \right);f\left( b \right);f\left( c \right)>0\,\,\forall a;b;c\in \left[ 1;3 \right]\Rightarrow -m+4>0\Leftrightarrow m>4\)

Theo yêu cầu của bài toán ta có : 

\(\left[ \begin{array}{l}g\left( a \right) + g\left( b \right) + m > g\left( c \right)\\g\left( b \right) + g\left( c \right) + m > g\left( a \right)\\g\left( a \right) + g\left( c \right) + m > g\left( b \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > g\left( c \right) - \left[ {g\left( a \right) + g\left( b \right)} \right]\\m > g\left( a \right) - \left[ {g\left( b \right) + g\left( c \right)} \right]\\m > g\left( b \right) - \left[ {g\left( a \right) + g\left( c \right)} \right]\end{array} \right.\)

Vì a, b, c đóng vai trò như nhau nên ta có thể nói \(m>g\left( a \right)-\left[ g\left( b \right)+g\left( c \right) \right]\,\,\,\forall a,b,c\in \left[ 1;3 \right]\)

Theo giả thiết a, b, c phân biệt \(\Rightarrow m\ge \underset{\left[ 1;3 \right]}{\mathop{\max }}\,g\left( x \right)-2\underset{\left[ 1;3 \right]}{\mathop{\min }}\,g\left( x \right)=0-2.4=8\)

Kết hợp điều kiện đề bài cho ta có \(8\le m\le 2018\Rightarrow \) Có 2011 giá trị nguyên của m thỏa mãn.

Chọn A.