Phương pháp giải:

Phương trình tiếp tuyến của đồ thị hàm số \(y=f\left( x \right)\) tại điểm có hoành độ \({{x}_{0}}:\,\,y=f'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+{{y}_{0}}\).

Lời giải chi tiết:

TXĐ \(D=R\backslash \left\{ 1 \right\}\)

Ta có: \(y'=\frac{-1}{{{\left( 1-x \right)}^{2}}}\)

\(\Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \({{x}_{0}}\) là:

\(y=\frac{-1}{{{\left( 1-{{x}_{0}} \right)}^{2}}}\left( x-{{x}_{0}} \right)+\frac{{{x}_{0}}-2}{1-{{x}_{0}}}\,\,\left( d \right)\)

\(\begin{align}  A\left( m;1 \right)\in d\Rightarrow 1=-\frac{1}{{{\left( 1-{{x}_{0}} \right)}^{2}}}\left( m-{{x}_{0}} \right)+\frac{{{x}_{0}}-2}{1-{{x}_{0}}} \\  \Leftrightarrow 1=\frac{-m+{{x}_{0}}-x_{0}^{2}+3{{x}_{0}}-2}{{{\left( 1-{{x}_{0}} \right)}^{2}}} \\  \Leftrightarrow -x_{0}^{2}+4{{x}_{0}}-m-2=x_{0}^{2}-2{{x}_{0}}+1 \\  \Leftrightarrow 2x_{0}^{2}-6{{x}_{0}}+m+3=0 \\  \Leftrightarrow 2x_{0}^{2}-6{{x}_{0}}+3=-m\,\,\,\left( * \right) \\ \end{align}\)

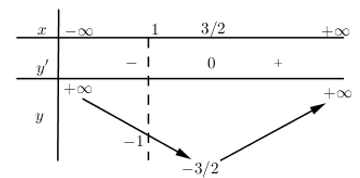
Xét hàm số \(f\left( x \right)=2{{x}^{2}}-6x+3\,\,\,\left( x\ne 1 \right)\) ta có: \(f'\left( x \right)=4x-6=0\Leftrightarrow x=\frac{3}{2}\)

BBT :

Để có đúng 1 tiếp tuyến qua A thì phương trình (*) có nghiệm duy nhất

\( \Rightarrow \left[ \begin{array}{l} - m = \frac{{ - 3}}{2}\\ - m =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \frac{3}{2}\\m = 1\end{array} \right. \Rightarrow S = \frac{9}{4} + 1 = \frac{{13}}{4}\)

Chọn A.