Câu hỏi
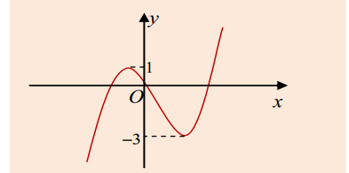
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị như hình vẽ
Tìm tất cả các giá trị của m để hàm số \(y=\left| f\left( x \right)+m \right|\) có ba điểm cực trị.
- A
\(m\ge 3\) hoặc \(m\le -1.\)
- B
\(m\ge 1\) hoặc \(m\le -3.\)
- C
\(m=3\) hoặc \(m=-1.\)
- D \(1\le m\le 3.\)
Phương pháp giải:
Dựa vào đồ thị hàm số \(y=f\left( x \right)\) suy ra các giá trị cực trị của đồ thị hàm số \(y=f\left( x \right)+m\)và dựa vào cách vẽ đồ thị hàm số \(y=\left| f\left( x \right)+m \right|\).
Lời giải chi tiết:
Đồ thị hàm số \(y=f\left( x \right)+m\)có được bằng cách tịnh tiến đồ thị hàm số \(y=f\left( x \right)\) lên trên theo phương của trục Oy m đơn vị, do đó nó đồ thị hàm số \(y=f\left( x \right)+m\)có \({{x}_{CD}}=1+m;\,\,{{x}_{CT}}=-3+m\)
Để đồ thị hàm số \(y=\left| f\left( x \right)+m \right|\) có ba cực trị thì
\(\left[ \begin{array}{l}{y_{CT}} = - 3 + m \ge 0\\{y_{CD}} = 1 + m \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \ge 3\\m \le - 1\end{array} \right.\)
Chọn A.