Câu hỏi
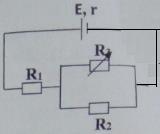
Cho sơ đồ mạch điện như hình vẽ: r = 2Ω, R1 = 4Ω, R2 = 6Ω, R3 là một biến trở. Thay đổi biến trở R3 đến giá trị nào thì công suất trên R3 đạt giá trị cực đại
- A 1Ω
- B 3Ω.
- C 4Ω.
- D 2Ω
Phương pháp giải:
Sử dụng công thức tính công suất tỏa nhiệt trên điện trở, bất đẳng thức Cô-si
Lời giải chi tiết:
Cường độ dòng điện trong mạch kín được tính theo công thức
\(I = \frac{E}{{{R_1} + \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} + r}} = \frac{E}{{6 + \frac{{6{R_3}}}{{6 + {R_3}}}}} = \frac{{E\left( {{R_3} + 6} \right)}}{{12{R_3} + 36}}\)
Ta có \({U_{23}} = I{R_{23}} = \frac{{E\left( {{R_3} + 6} \right)}}{{12{R_3} + 36}}.\frac{{6{R_3}}}{{{R_3} + 6}} = \frac{{E.6{R_3}}}{{12{R_3} + 36}}\)
Công suất tỏa nhiệt trên điện trở R3 được tính theo công thức
\[{P_3} = \frac{{U_3^2}}{{{R_3}}} = \frac{{U_{23}^2}}{{{R_3}}} = \frac{{{{\left( {\frac{{E.6{R_3}}}{{12{R_3} + 36}}} \right)}^2}}}{{{R_3}}} = \frac{{36E{R_3}}}{{{{\left( {12 + 36{R_3}} \right)}^2}}} = \frac{{3E}}{{12{{\left( {\frac{1}{{\sqrt {{R_3}} }} + 3\sqrt {{R_3}} } \right)}^2}}}\]
Để P3max thì \[{\left( {\frac{1}{{\sqrt {{R_3}} }} + 3\sqrt {{R_3}} } \right)_{\min }} \Rightarrow \frac{1}{{\sqrt {{R_3}} }} = 3\sqrt {{R_3}} \](theo bất đẳng thức Cô-si)
Suy ra R3 = 3Ω
Chọn B