Câu hỏi
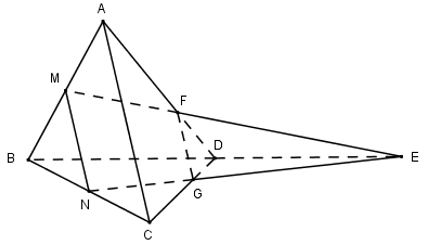
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V?
- A \(\frac{\sqrt{2}{{a}^{3}}}{18}\)
- B \(\frac{13\sqrt{3}{{a}^{3}}}{216}\)
- C \(\frac{7\sqrt{2}{{a}^{3}}}{216}\)
- D \(\frac{11\sqrt{2}{{a}^{3}}}{216}\)
Phương pháp giải:
Tính thể tích của phần khối đa diện không chứa điểm A theo thể tích của khối tứ diện ABCD sau đó suy ra V.
Lời giải chi tiết:
Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Gọi thể tích của phần đa diện còn lại là \(V'\)
Gọi \(F=EM\cap AD;\,\,G=EN\cap CD\)
Áp dụng định lí Menelaus trong tam giác BCD có: \(\frac{NB}{NC}.\frac{GC}{GD}.\frac{ED}{EB}=1\Rightarrow \frac{GC}{GD}=2\)
Áp dụng định lí Menelaus trong tam giác ABD có: \(\frac{MA}{MB}.\frac{EB}{ED}.\frac{FD}{FA}=1\Rightarrow \frac{FD}{FA}=\frac{1}{2}\)
Ta có \({{S}_{\Delta EBN}}=\frac{1}{2}d\left( E;BN \right).BN=\frac{1}{2}.2d\left( D;BC \right).\frac{1}{2}BC=\frac{1}{2}d\left( D;BC \right).BC={{S}_{\Delta BCD}}\)
\(\begin{align} d\left( M;\left( EBN \right) \right)=\frac{1}{2}d\left( A;\left( BCD \right) \right)\Rightarrow {{V}_{M.EBN}}=\frac{1}{2}{{V}_{ABCD}} \\ {{S}_{\Delta EDG}}=\frac{1}{2}d\left( G;DE \right).DE=\frac{1}{2}.\frac{1}{3}d\left( C;BD \right).BD=\frac{1}{3}.\frac{1}{2}d\left( C;BD \right).BD=\frac{1}{3}{{S}_{\Delta BCD}} \\ d\left( F;\left( EDG \right) \right)=\frac{1}{3}d\left( A;\left( BCD \right) \right)\Rightarrow {{V}_{M.EBN}}=\frac{1}{9}{{V}_{ABCD}} \\ \Rightarrow V'={{V}_{M.EBN}}-{{V}_{M.EBN}}=\frac{7}{18}{{V}_{ABCD}}\Rightarrow V=\frac{11}{18}{{V}_{ABCD}} \\ \end{align}\)
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD ta có \(AH\bot \left( BCD \right)\) và \(BH=\frac{2}{3}\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)
\(\begin{align} \Rightarrow AH=\sqrt{{{a}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}}=\frac{a\sqrt{6}}{3}\Rightarrow {{V}_{ABCD}}=\frac{1}{3}AH.{{S}_{BCD}}=\frac{1}{3}\frac{a\sqrt{6}}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{2}}{12} \\ \Rightarrow V=\frac{11}{18}.\frac{{{a}^{3}}\sqrt{2}}{12}=\frac{11\sqrt{2}{{a}^{3}}}{216} \\ \end{align}\)
Chọn D.