Câu hỏi
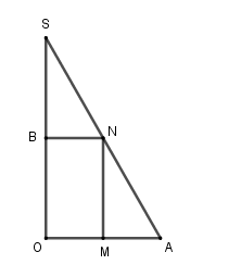
Cho tam giác SOA vuông tại O có MN // SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt \(SO=h\) không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình hón S có đáy là hình tròn tâm O bán kính \(R=OA\). Tìm độ dài MN theo h để thể tích khối trụ là lớn nhất.
- A \(MN=\frac{h}{2}\)
- B \(MN=\frac{h}{3}\)
- C \(MN=\frac{h}{4}\)
- D \(MN=\frac{h}{6}\)
Phương pháp giải:
Đặt \(OM=x\), tính MN theo h, R, x.
Tính thể tích khối trụ \({{V}_{tru}}=\pi {{R}^{2}}h\) trong đó \(R,h\) lần lượt là bán kính đáy và chiều cảo của khối trụ, tìm GTLN của thể tích đó.
Lời giải chi tiết:
Khi quay hình bên quanh cạnh SO ta được khối trụ đường cao MN, bán kính đáy OM nội tiếp khối nón đỉnh S, đường cao SO, bán kính đáy \(R=OA\).
Đặt \(OM=x\,\,\left( 0<x\le R \right)\) ta có:
\(\frac{MN}{h}=\frac{AM}{R}\Rightarrow \frac{h-MN}{h}=\frac{OA-AM}{R}=\frac{x}{R}\Rightarrow h-MN=h\frac{x}{R}\Leftrightarrow MN=h\left( 1-\frac{x}{R} \right)\)
\(\Rightarrow {{V}_{tru}}=\pi O{{M}^{2}}.MN=\pi .{{x}^{2}}.h\left( 1-\frac{x}{R} \right)=\frac{\pi h}{R}{{x}^{2}}\left( R-x \right)\)
Đặt \(f\left( x \right)={{x}^{2}}\left( R-x \right)=R{{x}^{2}}-{{x}^{3}}\) ta có \(f'\left( x \right)=2Rx-3{{x}^{2}}=0\Leftrightarrow \left[ \begin{align} x=0\,\,\,\left( ktm \right) \\ x=\frac{2R}{3}\,\,\left( tm \right) \\ \end{align} \right.\)
Dễ thấy \(\underset{\left( 0;R \right]}{\mathop{\max }}\,f\left( x \right)=f\left( \frac{2R}{3} \right)\Leftrightarrow x=\frac{2R}{3}=OM\)
\(\Rightarrow MN=h\left( 1-\frac{\frac{2R}{3}}{R} \right)=\frac{h}{3}\)
Chọn B.