Câu hỏi
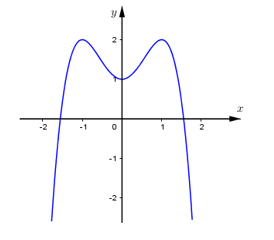
Đường cong hình bên là đồ thị của hàm số nào?
- A \(y=-{{x}^{4}}+1\)
- B \(y=-{{x}^{4}}+2{{x}^{2}}+1\)
- C \(y=-{{x}^{4}}-2{{x}^{2}}+1\)
- D \(y=-{{x}^{4}}+2{{x}^{2}}-1\)
Phương pháp giải:
Hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\left( a\ne 0 \right)\)
Nếu \(\left\{ \begin{align} \underset{x\to -\infty }{\mathop{\lim }}\,y=-\infty \Rightarrow a<0 \\ \underset{x\to -\infty }{\mathop{\lim }}\,y=+\infty \Rightarrow a>0 \\ \end{align} \right.\)
Và dựa vào các điểm mà đồ thị hàm số đi qua và các điểm cực trị của đồ thị hàm số.
Lời giải chi tiết:
Đồ thị hàm số có dạng \(y=a{{x}^{4}}+b{{x}^{2}}+c\,\,\left( a\ne 0 \right)\)
Ta có \(\underset{x\to -\infty }{\mathop{\lim }}\,y=-\infty \Rightarrow a<0\Rightarrow \) Chưa loại được đáp án.
Đồ thị hàm số đi qua \(\left( 0;1 \right)\Rightarrow c=1\Rightarrow \) Loại đáp án D.
Ta có \(y'=4a{{x}^{3}}+2bx=0\Leftrightarrow \left[ \begin{align} x=0 \\ {{x}^{2}}=-\frac{b}{a} \\ \end{align} \right.\)
Đồ thị hàm số có ba điểm cực trị \(\Leftrightarrow -\frac{b}{a}>0\Rightarrow \frac{b}{a}<0\Rightarrow b>0\Rightarrow \) Loại A và C.
Chọn B.