Câu hỏi
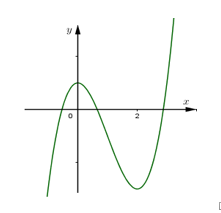
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ. Số cực trị của hàm số \(y=f({{x}^{2}}-2x)\)
- A 2
- B 5
- C 4
- D 3
Phương pháp giải:
Đạo hàm hàm hợp : \(y=f\left( u(x) \right)\,\,\Rightarrow \,\,y'=f'\left( u(x) \right).u'(x)\)
Lời giải chi tiết:
Dựa vào đồ thị hàm số \(y=f\left( x \right)\) ta thấy hàm số có hai điểm cực trị là \({{x}_{CT}}=2,\,\,{{x}_{CD}}=0\Rightarrow f'\left( x \right)=0\Leftrightarrow \left[ \begin{align} x=2 \\ x=0 \\ \end{align} \right.\)
\(y=f({{x}^{2}}-2x)\Rightarrow y'=f'({{x}^{2}}-2x).(2x-2)\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}f'({x^2} - 2x) = 0\\2x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2x = 0\\{x^2} - 2x = 2\\x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = 1 \pm \sqrt 3 \\x = 1\end{array} \right.\)
Vậy, hàm số \(y=f({{x}^{2}}-2x)\) có 5 cực trị.
Chọn: B