Câu hỏi
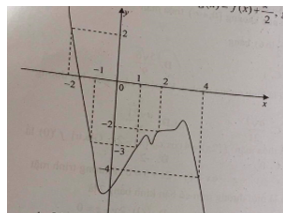
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\) đồ thị hàm số \(y=f'(x)\) như hình vẽ. Biết \(f(2)=-6,\,\,f(-4)=-10\) và hàm số \(g(x)=f(x)+\frac{{{x}^{2}}}{2}\), \(g(x)\) có ba điểm cực trị. Phương trình \(g(x)=0\)?
- A Có đúng 2 nghiệm.
- B Vô nghiệm.
- C Có đúng 3 nghiệm.
- D Có đúng 4 nghiệm.
Phương pháp giải:
Lập bảng biến thiên của \(g(x)\) và đánh giá số giao điểm của đồ thị hàm số \(y=g(x)\) và trục hoành.
Lời giải chi tiết:

\(g(x)=f(x)+\frac{{{x}^{2}}}{2}\Rightarrow g'(x)=f'(x)+x\)
\(g'(x)=0\Leftrightarrow f'(x)=-x\)
Xét giao điểm của đồ thị hàm số \(y=f'(x)\) và đường thẳng \(y=-x\) ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: \(-2;\,\,2;\,\,4\) tương ứng với 3 điểm cực trị của \(y=g(x)\).
\(g(2)=f(2)+\frac{{{2}^{2}}}{2}=-6+2=-4;\,\,g(-4)=f(-4)+\frac{{{(-4)}^{2}}}{2}=-10+8=-2\)
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy \(g\left( x \right)<0\,\,\forall x\in \left( 2;4 \right)\Rightarrow \) phương trình \(g\left( x \right)=0\) không có nghiệm \(x\in \left( 2;4 \right)\).
Chọn: B.