Câu hỏi
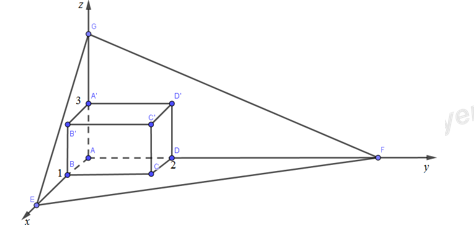
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 1, BC = 2, AA’ = 3. Mặt phẳng (P) thay đổi và luôn đi qua C’, mặt phẳng (P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Tính tổng \(T=AE+AF+AG\) sao cho thể tích khối tứ diện AEFG nhỏ nhất.
- A 15
- B 16
- C 17
- D
18
Phương pháp giải:
Sử dụng phương pháp tọa độ hóa.
Lời giải chi tiết:
Gắn hệ trục Oxyz, có các tia Ox, Oy, Oz lần lượt trùng với các tia AB, AD, AA’.
\(A(0;0;0),\,\,B(1;0;0),\,\,C(1;2;0),\,\,D(0;2;0),\,\,A'(0;0;3),\,\,B'(1;0;3),\,C'(1;2;3),\,\,D'(0;2;3)\)
(P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Gọi \(E(a;0;0),\,F(0;b;0),G(0;0;c),\,\,\left( a,b,c>0 \right)\)
Phương trình mặt phẳng (P): \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
\(C'(1;2;3)\in \left( P \right)\Rightarrow \frac{1}{a}+\frac{2}{b}+\frac{3}{c}=1\)
Thể tích tứ diện AEFG: \(V=\frac{1}{6}AE.AF.AG=\frac{1}{6}abc\).
Ta có: \(\frac{1}{a}+\frac{2}{b}+\frac{3}{c}\ge 3.\sqrt[3]{\frac{1}{a}.\frac{2}{b}.\frac{3}{c}}\Leftrightarrow 1\ge \frac{3\sqrt[3]{6}}{\sqrt[3]{abc}}\Leftrightarrow \sqrt[3]{abc}\ge 3\sqrt[3]{6}\Leftrightarrow abc\ge 162\Leftrightarrow \frac{1}{6}abc\ge 27\Leftrightarrow V\ge 27\)
\(\Rightarrow {{V}_{\min }}=27\) khi và chỉ khi \(\left\{ \begin{array}{l}\frac{1}{a} = \frac{2}{b} = \frac{3}{c}\\\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 6\\c = 9\end{array} \right.\)
Khi đó, \(T=AE+AF+AG=a+b+c=3+6+9=18\)
Chọn: D