Câu hỏi
Cho hàm số \(y=f(x)\). Hàm số \(y=f'(x)\) có đồ thị như hình bên. Hàm số \(y=f({{x}^{2}})\) đồng biến trên khoảng.
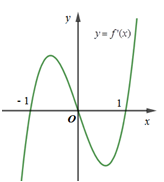
- A
\(\left( 1;+\infty \right)\).
- B
\(\left( -1;+\infty \right)\).
- C
\(\left( -\infty ;-1 \right)\).
- D \(\left( -1;1 \right)\).
Phương pháp giải:
Tính \(y'\), giải bất phương trình \(y'>0\)
Lời giải chi tiết:
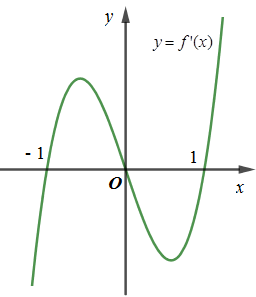
\(y=f\left( {{x}^{2}} \right)\Rightarrow y'=f'\left( {{x}^{2}} \right).2x=2xf'\left( {{x}^{2}} \right)\)
Với \(x\in \left( 1;+\infty \right)\Rightarrow x>0\)
\(\Rightarrow {{x}^{2}}\in \left( 1;+\infty \right)\Rightarrow f'\left( {{x}^{2}} \right)>0\Rightarrow y'>0\,\,\forall x\in \left( 1;+\infty \right)\)
Chọn: A
Câu hỏi trước
