Câu hỏi
Biết rằng đồ thị hàm số bậc 4: \(y=f\left( x \right)\) được cho như hình vẽ sau:
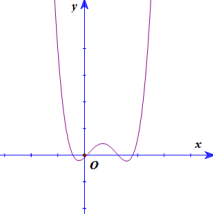
Tìm số giao điểm của đồ thị hàm số \(y=g\left( x \right)={{\left[ f'\left( x \right) \right]}^{2}}-f\left( x \right).f''\left( x \right)\) và trục Ox.
- A 0
- B 2
- C 4
- D 6
Phương pháp giải:
Đặt \(f\left( x \right)=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\left( x-{{x}_{3}} \right)\left( x-{{x}_{4}} \right)\), tính đạo hàm của hàm số \(y=f\left( x \right)\)
Xét hàm số \(h\left( x \right)=\frac{f'\left( x \right)}{f\left( x \right)}\) và chứng minh \(f''\left( x \right).f\left( x \right)-{{\left[ f'\left( x \right) \right]}^{2}}<0\,\,\forall x\notin \left\{ {{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\}\) .
Lời giải chi tiết:
Đồ thị hàm số \(y=f\left( x \right)\) cắt trục hoành tại bốn điểm phân biệt nên \(f\left( x \right)=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\left( x-{{x}_{3}} \right)\left( x-{{x}_{4}} \right)\)
\(\begin{align} \Rightarrow f'\left( x \right)=a\left( x-{{x}_{2}} \right)\left( x-{{x}_{3}} \right)\left( x-{{x}_{4}} \right)+a\left( x-{{x}_{1}} \right)\left( x-{{x}_{3}} \right)\left( x-{{x}_{4}} \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\left( x-{{x}_{4}} \right)+a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\left( x-{{x}_{3}} \right) \\ f'\left( x \right)=f\left( x \right)\left( \frac{1}{x-{{x}_{1}}}+\frac{1}{x-{{x}_{2}}}+\frac{1}{x-{{x}_{3}}}+\frac{1}{x-{{x}_{4}}} \right)\,\,\,\forall x\notin \left\{ {{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\}\Rightarrow f'\left( x \right)\ne 0\,\,\forall x\notin \left\{ {{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\} \\ \end{align}\)
Đặt \(h\left( x \right)=\frac{f'\left( x \right)}{f\left( x \right)}=\frac{1}{x-{{x}_{1}}}+\frac{1}{x-{{x}_{2}}}+\frac{1}{x-{{x}_{3}}}+\frac{1}{x-{{x}_{4}}}\,\,\forall x\notin \left\{ {{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\}\)
Ta có \(h'\left( x \right)=\frac{f''\left( x \right).f\left( x \right)-{{\left[ f'\left( x \right) \right]}^{2}}}{{{f}^{2}}\left( x \right)}=\frac{-1}{{{\left( x-{{x}_{1}} \right)}^{2}}}+\frac{-1}{{{\left( x-{{x}_{2}} \right)}^{2}}}+\frac{-1}{{{\left( x-{{x}_{3}} \right)}^{2}}}+\frac{-1}{{{\left( x-{{x}_{4}} \right)}^{2}}}<0\,\,\forall x\notin \left\{ {{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\}\)
\(\begin{align} \Rightarrow f''\left( x \right).f\left( x \right)-{{\left[ f'\left( x \right) \right]}^{2}}<0\,\,\forall x\notin \left\{ {{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\} \\ \Rightarrow g\left( x \right)={{\left[ f'\left( x \right) \right]}^{2}}-f''\left( x \right).f\left( x \right)>0\,\,\forall x\notin \left\{ {{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}} \right\} \\ \end{align}\)
Khi \(f\left( x \right)=0\Rightarrow f'\left( x \right)\ne 0\Rightarrow g\left( x \right)={{\left[ f'\left( x \right) \right]}^{2}}-f''\left( x \right).f\left( x \right)\ne 0\)
Vậy đồ thị hàm số \(y=g\left( x \right)={{\left[ f'\left( x \right) \right]}^{2}}-f\left( x \right).f''\left( x \right)\) không cắt trục Ox.
Chọn A.







