Câu hỏi
Cho hàm số \(y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\,\left( a;b;c;d\in R,\,\,a\ne 0 \right)\) có đồ thị \(\left( C \right)\). Biết rằng đồ thị \(\left( C \right)\) đi qua gốc tọa độ và có đồ thị hàm số \(y=f'\left( x \right)\) cho bởi hình vẽ sau đây.
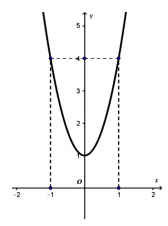
Tính giá trị \(H=f\left( 4 \right)-f\left( 2 \right)\).
- A
\(H=51\)
- B
\(H=45\)
- C
\(H=58\)
- D \(H=64\)
Phương pháp giải:
Xác định hàm số \(f'\left( x \right)\) từ đó tính được \(f\left( x \right)=\int\limits_{{}}^{{}}{f'\left( x \right)dx}\).
Lời giải chi tiết:
Ta dễ dàng tìm được phương trình parabol là \(y=3{{x}^{2}}+1\Rightarrow f'\left( x \right)=3{{x}^{2}}+1\Rightarrow f\left( x \right)=\int\limits_{{}}^{{}}{f'\left( x \right)dx}={{x}^{3}}+x+C\)
Đồ thị hàm số đi qua gốc tọa độ \(\Rightarrow C=0\Rightarrow f\left( x \right)={{x}^{3}}+x\)
\(\Rightarrow f\left( 4 \right)=68;\,\,f\left( 2 \right)=10\Rightarrow H=58\).
Chọn C.
Câu hỏi trước
