Câu hỏi
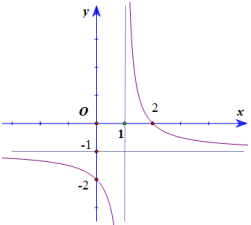
Cho hàm số \(y=\frac{ax+b}{x+c}\) có đồ thị như hình vẽ, a, b, c là các số nguyên. Tính giá trị của biểu thức \(T=a-3b+2c\).
- A
\(T=-9\)
- B
\(T=-7\)
- C
\(T=12\)
- D \(T=10\)
Phương pháp giải:
Dựa vào các đường tiệm cận và các điểm đi qua của đồ thị hàm số.
Lời giải chi tiết:
Đồ thị hàm số có đường TCĐ \(x=-c\Rightarrow -c=1\Leftrightarrow c=-1\), TCN \(y=a\Rightarrow a=-1\).
Đồ thị hàm số đi qua \(\left( 0;-2 \right)\Rightarrow -2=\frac{b}{c}\Rightarrow b=-2c=2\).
\(\Rightarrow T=a-3b+2c=-1-3.2+2\left( -1 \right)=-9\).
Chọn A.
Câu hỏi trước
