Câu hỏi
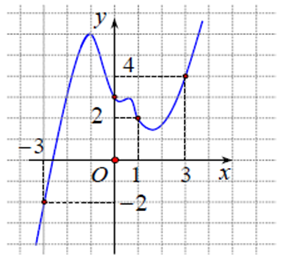
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}.\) Đồ thị của hàm số \(y={f}'\left( x \right)\) như hình bên. Đặt \(g\left( x \right)=2f\left( x \right)-{{\left( x+1 \right)}^{2}}.\) Mệnh đề nào dưới đây đúng?
- A \(\underset{\left( -\,3;\,3 \right)}{\mathop{\min }}\,\,g\left( x \right)=g\left( 1 \right).\)
- B \(\underset{\left( -\,3;\,3 \right)}{\mathop{\max }}\,\,g\left( x \right)=g\left( 1 \right).\)
- C \(\underset{\left( -\,3;\,3 \right)}{\mathop{\min }}\,\,g\left( x \right)=g\left( 3 \right).\)
- D Không tồn tại giá trị nhỏ nhất của \(g\left( x \right)\) trên \(\left( -\,3;\,3 \right).\)
Phương pháp giải:
+) Từ độ thị hàm số \(y=f'\left( x \right)\) tìm các điểm \({{x}_{0}}\) mà tại đó \(g'\left( {{x}_{0}} \right)=0\)
+) Xác định các khoảng đơn điệu của đồ thị hàm số \(y=g\left( x \right)\).
+) Lập BBT của đồ thị hàm số \(y=g\left( x \right)\)
Lời giải chi tiết:
Ta có: \(g'\left( x \right)=2f'\left( x \right)-2\left( x+1 \right)=0\Leftrightarrow \left[ \begin{align} & x=-3 \\ & x=1 \\ & x=3 \\ \end{align} \right.\)
Với \(x<-3\) ta có: \(f'\left( x \right)<x+1\) suy ra hàm số nghịch biến trên khoảng \(\left( -\infty ;-3 \right)\)
Bảng xét dấu của \({g}'\left( x \right)\)
Dựa vào bảng xét dấu, ta được \(\underset{\left( -\,3;3 \right)}{\mathop{\max }}\,g\left( x \right)=g\left( 1 \right).\)
Chọn B.