Câu hỏi
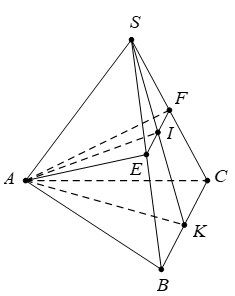
Cho hình chóp đều \(S.\,ABC\) có đáy là tam giác đều cạnh \(a.\) Gọi \(E,\,\,F\) lần lượt là trung điểm của các cạnh \(SB,\,\,SC.\) Biết mặt phẳng \(\left( AEF \right)\) vuông góc với mặt phẳng \(\left( SBC \right).\) Tính thể tích khối chóp \(S.\,ABC.\)
- A \(\frac{{{a}^{3}}\sqrt{5}}{24}.\)
- B \(\frac{{{a}^{3}}\sqrt{5}}{8}.\)
- C \(\frac{{{a}^{3}}\sqrt{3}}{24}.\)
- D \(\frac{{{a}^{3}}\sqrt{6}}{12}.\)
Phương pháp giải:
Gọi H là tâm tam giác đều ABC ta có \(SH\bot \left( ABC \right)\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{ABC}}\).
Lời giải chi tiết:
Gọi \(K\) là trung điểm của \(BC\) và \(I=SK\cap EF.\)
Từ gt \(\Rightarrow \,\,EF=\frac{1}{2}BC=\frac{a}{2},\)\(EF\)//\(BC\)\(\Rightarrow \,\,I\) là trung điểm của \(SK\) và \(EF.\)
Ta có \(\Delta \,SAB=\Delta \,SAC\)\(\Rightarrow \) Hai trung tuyến tương ứng \(AE=AF.\)
\(\Rightarrow \) Tam giác \(AEF\) cân tại \(A\,\,\Rightarrow \,\,AI\bot EF\)
Mặt khác \(\left( SBC \right)\bot \left( AEF \right)\Rightarrow AI\bot \left( SBC \right)\Rightarrow AI\bot SK.\)
Suy ra \(\Delta \,SAK\) cân tại \(A\,\,\Rightarrow \,\,SA=AK=\frac{a\sqrt{3}}{2}.\)
Gọi H là tâm tam giác đều ABC ta có \(SH\bot \left( ABC \right)\) và \(AH=\frac{2}{3}\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)
\(\Rightarrow SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}}=\frac{a\sqrt{15}}{6}\)
Vậy thể tích khối chóp \(S.ABC\) là \(V=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{1}{3}.\frac{a\sqrt{15}}{6}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{5}}{24}.\)
Chọn A.