Câu hỏi
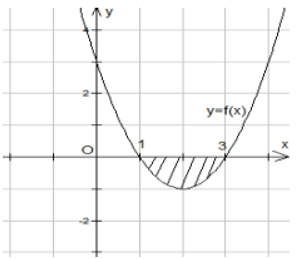
Cho hàm số \(y=f\left( x \right)\) liên tục và có đồ thị như hình bên. Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục \(Ox.\) Quay hình phẳng \(D\) quanh trục \(Ox\) ta được khối tròn xoay có thể tích \(V\) được xác định theo công thức
- A \(V={{\pi }^{2}}\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
- B \(V=\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
- C \(V=\frac{1}{3}\int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
- D \(V=\pi \int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
Phương pháp giải:
Công thức tính thể tích của khối tròn xoay là \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\,\text{d}x}\)
Lời giải chi tiết:
Thể tích khối tròn xoay cần tính là \(V=\pi \int\limits_{1}^{3}{{{\left[ f\left( x \right) \right]}^{\,2}}\,\text{d}x}.\)
Chọn D
Câu hỏi trước
