Câu hỏi
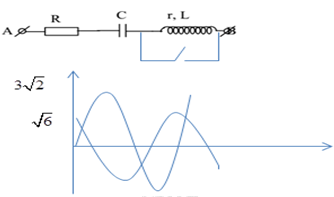
Cho mạch điện như hình vẽ, cuộn dây thuần cảm, r = 0. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị cực đại \({U_0} = 100\sqrt 6 V\), tần số f = 50 Hz. Khi K mở hoặc đóng, thì đồ thị cường độ dòng điện qua mạch theo thời gian tương ứng là im và id được biểu diễn như hình bên. Điện trở các dây nối rất nhỏ. Giá trị của R bằng
- A 100 Ω.
- B \(100\sqrt 3 \Omega \)
- C \(50\sqrt 3 \Omega \)
- D 50 Ω.
Phương pháp giải:
Sử dụng giản đồ vecto và các công thức lượng giác, hệ số công suất.
Lời giải chi tiết:
Từ đồ thị ta thấy
\(\eqalign{
& {I_d} = {{\sqrt 6 } \over {\sqrt 2 }} = \sqrt 3 A \Rightarrow {Z_d} = {U \over {{I_d}}} = {{100\sqrt 3 } \over {\sqrt 3 }} = 100\Omega \cr
& {I_m} = {{3\sqrt 2 } \over {\sqrt 2 }} = 3A \Rightarrow {Z_m} = {U \over {{I_m}}} = {{100\sqrt 3 } \over 3} = {{100} \over {\sqrt 3 }}\Omega \cr} \)
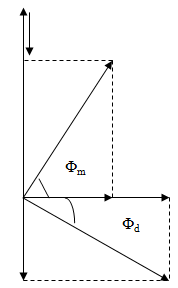
Khi đóng và mở khóa K thì cường độ dòng điện lệch pha nhau 1 góc là 900.
Ta vẽ trên một giản đồ vecto khi đóng và mở khóa K:
Từ công thức tính hệ số công suất ta có:
\(\eqalign{
& \cos {\varphi _d} = {R \over {{Z_d}}};\cos {\varphi _m} = {R \over {{Z_m}}};{\varphi _d} + {\varphi _m} = {\pi \over 2} \Rightarrow \cos {\varphi _d} = \sin {\varphi _m} = \sqrt {1 - {{\cos }^2}{\varphi _m}} \cr
& \Rightarrow {\left( {{R \over {{{100} \over {\sqrt 3 }}}}} \right)^2} = 1 - {\left( {{R \over {100}}} \right)^2} \Leftrightarrow {{3.{R^2}} \over {{{100}^2}}} = 1 - {{{R^2}} \over {{{100}^2}}} \Leftrightarrow 4.{R^2} = {100^2} \Rightarrow R = \sqrt {{{{{100}^2}} \over 4}} = 50\Omega \cr} \)