Phương pháp giải:

Dựng hình, xác định khoảng cách giữa hai đường thẳng chéo nhau để tính chiều cao lăng trụ

Lời giải chi tiết:

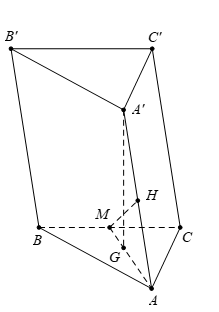
Gọi \(M\) là trung điểm của \(BC.\) Ta có \(\left\{ \begin{align}  {A}'G\bot BC \\ AM\bot BC \\\end{align} \right.\Rightarrow \,\,BC\bot \left( {A}'AM \right).\)

Kẻ \(MH\bot A{A}'\,\,\,\,\left( H\in A{A}' \right)\)\(\Rightarrow \)\(MH\) là đoạn vuông góc chung của \(BC,\,\,A{A}'.\)

\(\Rightarrow d\left( BC;AA' \right)=MH=\frac{a\sqrt{3}}{4}\)

Mà \(d=d\left( G;\left( A{A}' \right) \right)=\frac{2}{3}d\left( M;\left( A{A}' \right) \right)=\frac{2}{3}MH=\frac{a\sqrt{3}}{6}.\)

Xét tam giác vuông AA’G có :  \(\frac{1}{A{{G}^{2}}}+\frac{1}{{A}'{{G}^{2}}}=\frac{1}{{{d}^{2}}}\Rightarrow {A}'G=\frac{a}{3}.\)

Vậy thể tích cần tính là

\({{V}_{ABC.{A}'{B}'{C}'}}={A}'G\,\,\times \,\,{{S}_{\Delta \,ABC}}=\frac{a}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{3}}{12}.\)

Chọn B.