Phương pháp giải:

Viết phương trình tiếp tuyến, sử dụng điều kiện song song và yêu cầu bài toán tìm m

Lời giải chi tiết:

Gọi \(M\left( a;b \right)\in \left( C \right),\) ta có \({f}'\left( x \right)=2{{x}^{3}}-3{{x}^{2}}-12x\)\(\Rightarrow \,\,{f}'\left( a \right)=2{{a}^{3}}-3{{a}^{2}}-12a.\)

Suy ra phương trình tiếp tuyến của \(\left( C \right)\) tại \(M\) là \(y-f\left( a \right)={f}'\left( a \right)\left( x-a \right)\)        \(\left( \Delta  \right).\)

Vì \(\left( \Delta  \right)\) song song với \(d\)\(\Rightarrow \,\,\left\{ \begin{align}  {f}'\left( a \right)=m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \\ -\,a.{f}'\left( a \right)+f\left( a \right)\ne 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \\\end{align} \right..\)

Giải \(\left( 2 \right),\) ta có \(a.{f}'\left( a \right)+f\left( a \right)=\)\(-\,3{{a}^{4}}+4{{a}^{3}}+12{{a}^{2}}+14\ne 0\Leftrightarrow \,\,\left\{ \begin{align}  a\ne {{a}_{1}}\notin \mathbb{Z} \\  a\ne {{a}_{2}}\notin \mathbb{Z} \\ \end{align} \right..\)

Giải \(\left( 1 \right),\) ta có \(m=g\left( a \right)=2{{a}^{3}}-3{{a}^{2}}-12a;\,\,\forall a\in \mathbb{R}.\) Có \({g}'\left( a \right)=6{{a}^{2}}-6a-12=0\Leftrightarrow \left[ \begin{align}  a=-\,1 \\  a=2 \\ \end{align} \right..\)

Bảng biến thiên

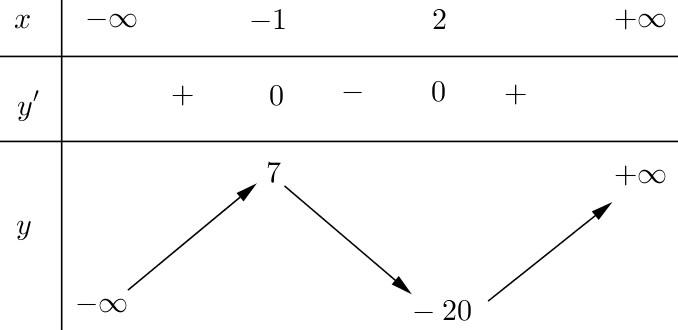
Dựa vào bảng biến thiên, để \(m=g\left( a \right)\) có ít nhất hai nghiệm \(\Leftrightarrow \,\,-\,20\le m\le 7.\)

Chọn D