Câu hỏi
Cho hai dao động điều hòa cùng phương, cùng tần số có phương trình tương ứng là x1 = A1cosωt cm; \({x_2} = {A_2}\cos \left( {\omega t + {\pi \over 3}} \right)\), tần số góc ω không đổi. Phương trình dao động tổng hợp của hai dao động trên là \(x = 2\sqrt 3 \cos \left( {\omega t + \varphi } \right)\,cm\). Giá trị lớn nhất của A1 + A2 là
- A \(4\sqrt 2 m\)
- B \(8\sqrt 2 m\)
- C 8 cm.
- D 4 cm.
Lời giải chi tiết:
Đáp án D
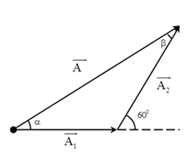
+ Biểu diễn vecto các dao động điều hòa.
Áp dụng định lý sin, ta có:
\({A \over {\sin 120^\circ }} = {{{A_1}} \over {\sin \beta }} = {{{A_2}} \over {\sin \alpha }} \to {A_1} + {A_2} = {A \over {\sin 120^\circ }}\left[ {\sin \alpha + \sin \beta } \right]\)
+ Biến đổi lượng giác:
\({A \over {\sin 120^\circ }}\left[ {\sin \alpha + \sin \beta } \right] = {{2{\rm{A}}} \over {\sin 120^\circ }}\left[ {\sin \left( {{{\alpha + \beta } \over 2}} \right)\cos \left( {{{\alpha - \beta } \over 2}} \right)} \right]\)
+ Với \(\alpha + \beta = 180^\circ - 120^\circ \).
\( \to {\left( {{A_1} + {A_2}} \right)_{\max }} = {{2A} \over {\sin 120^\circ }}\sin \left( {{{180^\circ - 120^\circ } \over 2}} \right) = 4\,\,cm.\)