Câu hỏi
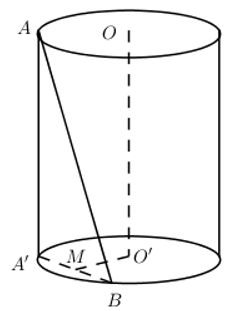
Cho hình trụ có chiều cao \(h=a\sqrt{3}\), bán kính đáy \(r=a\). Gọi \(O,O'\) lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
- A \(a\sqrt{6}\)
- B \(\frac{a\sqrt{6}}{2}\)
- C \(a\sqrt{3}\)
- D \(\frac{a\sqrt{3}}{2}\)
Phương pháp giải:
+) Xác định mặt phẳng (P) chứa AB và song song với OO’.
+) \(d\left( OO';AB \right)=d\left( OO';\left( P \right) \right)\)
Lời giải chi tiết:
Dựng \(AA'//OO'\) ta có : \(\widehat{\left( OO';AB \right)}=\widehat{\left( AA';AB \right)}=\widehat{A'AB}={{30}^{0}}\)
Gọi M là trung điểm của A’B ta có :
\(\left\{ \begin{align} & O'M\bot A'B \\ & O'M\bot AA' \\ \end{align} \right.\Rightarrow O'M\bot \left( ABA' \right)\Rightarrow O'M=d\left( O';\left( ABA' \right) \right)\)
\(\begin{align} & OO'//AA'\Rightarrow OO'//\left( ABA' \right)\supset AB\Rightarrow d\left( OO';AB \right)=d\left( OO';\left( ABA' \right) \right) \\ & =d\left( O'\left( ABA' \right) \right)=O'M \\ \end{align}\)
Xét tam giác vuông ABA’ có \(A'B=AA'.\tan 30=a\sqrt{3}.\frac{1}{\sqrt{3}}=a\)
\(\Rightarrow MB=\frac{a}{2}\)
Xét tam giác vuông O’MB có \(O'M=\sqrt{O'{{B}^{2}}-M{{B}^{2}}}=\frac{a\sqrt{3}}{2}\)
Chọn D.