Câu hỏi
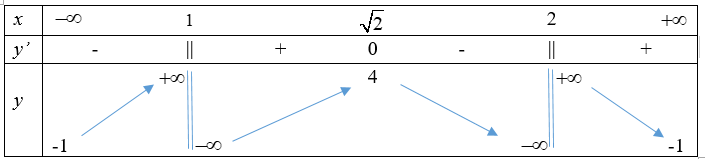
Cho hàm số \(y=f(x)\) liên tục trên \(R\text{ }\!\!\backslash\!\!\text{ }\left\{ 1;2 \right\}\) và có bảng biến thiên như sau
Phương trình \(f({{2}^{\sin \,x}})=3\) có bao nhiêu nghiệm trên \(\left[ 0;\frac{5\pi }{6} \right]\).
- A 3
- B 5
- C 2
- D 4
Lời giải chi tiết:
*) Phương trình \(f({{2}^{\sin \,x}})=3\) có nghiệm trên \(\left[ 0;\frac{5\pi }{6} \right]\Leftrightarrow \) \({{2}^{\sin \,x}}\le 4,\,\,x\in \left[ 0;\frac{5\pi }{6} \right]\).
* Xét hàm số \(y=g(x)={{2}^{\sin \,x}}\) trên \(\left[ 0;\frac{5\pi }{6} \right]\):
\(y'={{2}^{\sin \,x}}.\cos x\)
\(y'=0\Leftrightarrow \cos x=0\Leftrightarrow x=\frac{\pi }{2}+k\pi ,\,\,k\in \mathbb{Z}\)
Mà \(x\in \left[ 0;\frac{5\pi }{6} \right]\Rightarrow x=\frac{\pi }{2}\)
Bảng biến thiên:
+) Nếu \(x\in \left[ 0;\frac{\pi }{2} \right]\) thì \({{2}^{\sin \,x}}\) đơn điệu tăng từ 1 đến 2: Phương trình \(f({{2}^{\sin \,x}})=3\) có 2 nghiệm phân biệt trên đoạn này ( Nghiệm khác \(\frac{\pi }{2}\))
+) Nếu \(x\in \left[ \frac{\pi }{2};\frac{5\pi }{6} \right]\) thì \({{2}^{\sin \,x}}\) đơn điệu giảm từ 2 xuống \(\sqrt{2}\): Phương trình \(f({{2}^{\sin \,x}})=3\) có 1 nghiệm duy nhất trên đoạn này ( Nghiệm khác \(\frac{\pi }{2}\))
Vậy, trên \(\left[ 0;\frac{5\pi }{6} \right]\) phương trình \(f({{2}^{\sin \,x}})=3\) có tất cả 3 nghiệm.
Chọn: A