Phương pháp giải:

Phương pháp: Sử dụng công thức tính mức cường độ âm \(L = 10\log \frac{I}{{{I_0}}} = 10\log \frac{P}{{4\pi {r^2}{I_0}}}\)

Lời giải chi tiết:

Đáp án D

Cách giải:

+ Mức cường độ âm tại 1 điểm cách nguồn một khoảng r là: \(L = 10\log \frac{I}{{{I_0}}} = 10\log \frac{P}{{4\pi {r^2}{I_0}}}\)

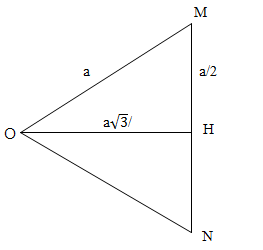
+ Để máy thu đặt tại một điểm trên đoạn MN thu được mức cường độ âm lớn nhất thì khoảng cách từ nguồn O đến điểm đó phải nhỏ nhất => điểm đó là điểm H (H là chân đường cao hạ từ O xuống MN).

+ Gọi độ dài các cạnh của ∆OMN là a.

Áp dụng định lí Pi – ta – go trong tam giác vuông OMH ta có: \(OH = \frac{{a\sqrt 3 }}{2}\)

+ Mức cường độ âm tại M và H:

\(\left\{ \matrix{
{L_M} = 10\log {P \over {4\pi .O{M^2}{I_0}}} \hfill \cr
{L_H} = 10\log {P \over {4\pi .O{H^2}{I_0}}} \hfill \cr} \right. \Rightarrow {L_H} - {L_M} = 20\log {{OM} \over {OH}} = 20\log {a \over {{{a\sqrt 3 } \over 2}}} = 1,25 \Rightarrow {L_H} = {L_M} + 1,25 = 24,77 + 1,25 = 26dB\)