Câu hỏi
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên \(\left( -\infty ;0 \right)\) và \(\left( 0;+\infty \right)\) có bảng biến thiên như sau:
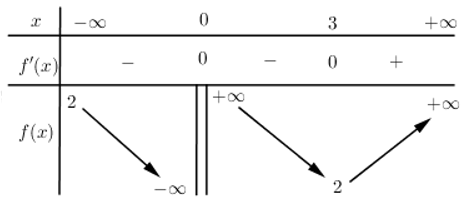
Mệnh đề nào dưới đây là đúng?
- A Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
- B Hàm số có giá trị nhỏ nhất bằng 2.
- C Hàm số đồng biến trên \(\left( 2;+\infty \right).\)
- D \(f\left( -3 \right)>f\left( -2 \right).\)
Phương pháp giải:
Dựa vào BBT, nhận xét từng đáp án.
Lời giải chi tiết:
Hàm số liên tục tại x = 2 \(\Rightarrow \underset{x\to 2}{\mathop{\lim }}\,f\left( x \right)=f\left( 2 \right)\Rightarrow \) x = 2 không là TCĐ của đồ thị hàm số \(\Rightarrow A\) sai.
\(\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f\left( x \right)=-\infty \Rightarrow B\) sai.
Hàm số đồng biến trên \(\left( 3;+\infty \right)\) và nghịch biến trên \(\left( 2;3 \right)\) do đó kết luận: Hàm số đồng biến trên \(\left( 2;+\infty \right)\) sai \(\Rightarrow C\) sai.
Ta thấy hàm số nghịch biến trên \(\left( -3;-2 \right)\Rightarrow f\left( -3 \right)>f\left( -2 \right)\Rightarrow D\) đúng.
Chọn D.







