Phương pháp giải:

Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác

Lời giải chi tiết:

- Phương trình dao động của x; x₁; x₂: 

\(\left\{ \matrix{
x = 5\cos \left( {\omega t + \varphi } \right) \hfill \cr
{x_1} = {A_1}\cos \left( {\omega t + {\pi \over 3}} \right) \hfill \cr
{x_2} = {A_2}\cos \left( {\omega t - {\pi \over 4}} \right) \hfill \cr} \right.\)

Suy ra :

+ Độ lệch pha giữa x và x₁ là : \({\pi  \over 3} - \varphi \)

+ Độ lệch pha giữa x và x₂ là : \(\varphi  + {\pi  \over 4}\)

+ Độ lệch pha giữa x₁ và x₂ là : \({\pi  \over 3} - \left( { - {\pi  \over 4}} \right) = {{7\pi } \over {12}}\)

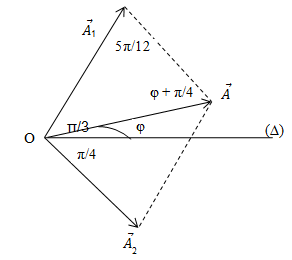
=> Ta có giản đồ vecto : 

- Áp dụng định lí hàm số sin trong tam giác ta có: 

\(\eqalign{
& {A \over {\sin {{5\pi } \over {12}}}} = {{{A_1}} \over {\sin (\varphi + {\pi \over 4})}} = {{{A_2}} \over {\sin ({\pi \over 3} - \varphi )}} \to \left\{ \matrix{
{A_1} = {{A\sin \left( {\varphi + {\pi \over 4}} \right)} \over {\sin {{5\pi } \over {12}}}} \hfill \cr
{A_2} = {{A\sin \left( {{\pi \over 3} - \varphi } \right)} \over {\sin {{5\pi } \over {12}}}} \hfill \cr} \right. \cr
& \to {A_1} + {A_2} = {{A\sin \left( {\varphi + {\pi \over 4}} \right)} \over {\sin {{5\pi } \over {12}}}} + {{A\sin \left( {{\pi \over 3} - \varphi } \right)} \over {\sin {{5\pi } \over {12}}}} = {A \over {\sin {{5\pi } \over {12}}}}\left[ {\sin \left( {\varphi + {\pi \over 4}} \right) + \sin \left( {{\pi \over 3} - \varphi } \right)} \right] \cr} \)

- Có : \(sina + sinb{\rm{ }} = 2\sin {{a + b} \over 2}.c{\rm{os}}{{a - b} \over 2} \Rightarrow \sin \left( {\varphi  + {\pi  \over 4}} \right) + \sin \left( {{\pi  \over 3} - \varphi } \right) = 2\sin {{7\pi } \over {24}}c{\rm{os}}\left( {\varphi  - {\pi  \over {24}}} \right)\)

\( \Rightarrow {A_1} + {A_2} = 2A{{\sin {{7\pi } \over {24}}} \over {\sin {{5\pi } \over {12}}}}.c{\rm{os}}\left( {\varphi  - {\pi  \over {24}}} \right)\) 

Để [A₁ + A₂] đạt cực đại thì: \({\left[ {c{\rm{os}}\left( {\varphi  - {\pi  \over {24}}} \right)} \right]_{{\rm{max}}}} = 1 \Rightarrow \varphi  - {\pi  \over {24}} = k2\pi  \Rightarrow \varphi  = {\pi  \over {24}}\)

Chọn B