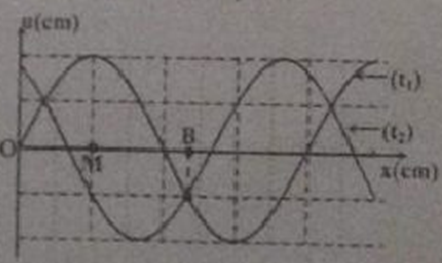Câu hỏi
Một sóng ngang có chu kì T (T > 4/15s), truyền trên mặt nước, dọc theo chiều dương trục Ox với vận tốc v = 240cm/s. Tại thời điểm t1 và \({t_2} = {t_1} + {4 \over {15}}(s)\) dạng mặt nước như hình vẽ. Trên mặt nước, hai điểm M, B là vị trí cân bằng của phần tử môi trường. Khoảng cách giữa hai điểm M, B là:
- A d = 44cm
- B d = 32cm
- C d = 36cm
- D d = 40cm
Phương pháp giải:
Sử dụng kĩ năng đọc đồ thì và công thức tính độ lệch pha \(\Delta \varphi = {{2\pi d} \over \lambda }\)
Lời giải chi tiết:
+ Xét điểm B tại hai thời điểm t1 và t2 thấy: B đi qua vị trí \(x = {{ - A} \over 2}\) và ngược chiều nhau, suy ra:
\({t_2} - {t_1} = {{2T} \over 3} = {4 \over {15}} \to T = 0,4s \to \lambda = 96cm\)
+ Tại thời điểm t2 thì M và B cùng li độ \(x = {{ - A} \over 2}\) suy ra độ lệch pha giữa hai điểm là: \(\Delta \varphi = {{2\pi d} \over \lambda } = {{2\pi } \over 3} \to d = {\lambda \over 3} = 32cm\)