Câu hỏi
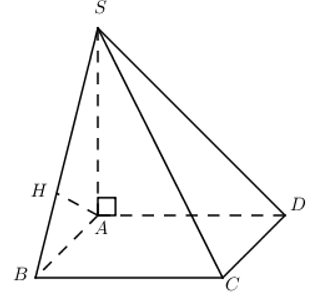
Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh a, SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng \(\frac{a\sqrt{2}}{2}\). Thể tích V của khối chóp đã cho.
- A \(V=\frac{{{a}^{3}}}{2}\)
- B \(V={{a}^{3}}\)
- C \(V=\frac{\sqrt{3}{{a}^{3}}}{9}\)
- D \(V=\frac{{{a}^{3}}}{3}\)
Phương pháp giải:
+) Xác định khoảng cách từ A đến (SBC).
+) Sử dụng hệ thức lượng trong tam giác vuông tính SA.
+) Tính thể tích khối chóp \(V=\frac{1}{3}SA.{{S}_{ABCD}}\).
Lời giải chi tiết:
Trong (SAB) kẻ \(AH\bot SB\) ta có :
\(\left\{ \begin{align} & BC\bot SA \\ & BC\bot AB \\ \end{align} \right.\Rightarrow BC\bot \left( SAB \right)\Rightarrow BC\bot AH\)
\(\Rightarrow AH\bot \left( SBC \right)\Rightarrow AH=\frac{a\sqrt{2}}{2}\)
Xét tam giác vuông SAB có :
\(\frac{1}{A{{H}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{B}^{2}}}\Leftrightarrow \frac{2}{{{a}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{{{a}^{2}}}\Leftrightarrow SA=a\)
Vậy \({{V}_{S.ABCD}}=\frac{1}{3}SA.{{S}_{ABCD}}=\frac{1}{3}a.{{a}^{2}}=\frac{{{a}^{3}}}{3}\)
Chọn D.