Câu hỏi
Cho hàm số \(y=f\left( x \right)\) xác định trên \(\left[ 0;+\,\infty \right),\) liên tục trên khoảng \(\left( 0;+\,\infty \right)\) và có bảng biến thiên như sau:
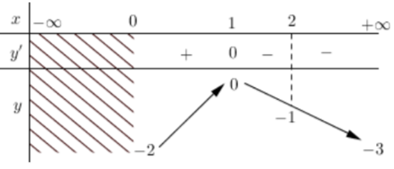
Tìm tập hợp tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(f\left( x \right)=m\) có hai nghiệm \({{x}_{1}},\,\,{{x}_{2}}\) thỏa mãn \({{x}_{1}}\in \left( 0;2 \right)\) và \({{x}_{2}}\in \left( 2;+\,\infty \right).\)
- A \(\left( -\,3;-\,1 \right).\)
- B \(\left( -\,2;-\,1 \right).\)
- C \(\left( -\,2;0 \right).\)
- D \(\left( -\,1;0 \right).\)
Phương pháp giải:
Dựa vào bảng biến thiên suy ra hình dáng đồ thị và biện luận theo số nghiệm của phương trình.
Lời giải chi tiết:
Dựa vào bảng biến thiên, ta thấy rằng:
Phương trình \(f\left( x \right)=m\) có hai nghiệm \({{x}_{1}},\,\,{{x}_{2}}\)\(\Leftrightarrow \)\(m\in \left( -\,2;0 \right)\)\(\Rightarrow \) Loại A. Phương trình \(f\left( x \right)=m\) có nghiệm \({{x}_{1}}\in \left( 0;2 \right)\)\(\Leftrightarrow \)\(m\in \left( -\,2;-\,1 \right).\) Phương trình \(f\left( x \right)=m\) có nghiệm \({{x}_{2}}\in \left( 2;+\,\infty \right)\)\(\Leftrightarrow \)\(m\in \left( -\,3;-\,1 \right).\)Kết hợp 3 điều kiện trên, ta được \(m\in \left( -\,2;-\,1 \right)\) là giá trị cần tìm.
Chọn B







