Lời giải chi tiết:

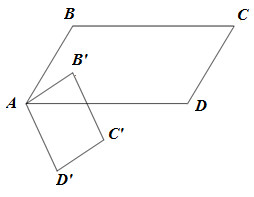
Gọi G là trọng tâm tam giác BC’D suy ra \(\overrightarrow {GB}  + \overrightarrow {GC'}  + \overrightarrow {GD}  = \overrightarrow 0 \).

\(\begin{array}{l} \Leftrightarrow \overrightarrow {GB'}  + \overrightarrow {B'B}  + \overrightarrow {GC}  + \overrightarrow {CC'}  + \overrightarrow {GD'}  + \overrightarrow {D'D}  = \overrightarrow 0 \\ \Leftrightarrow \left( {\overrightarrow {GB'}  + \overrightarrow {GC}  + \overrightarrow {GD'} } \right) + \left( {\overrightarrow {B'B}  + \overrightarrow {CC'}  + \overrightarrow {D'D} } \right) = \overrightarrow 0 \,\,\left( 1 \right)\end{array}\)

Mặt khác theo quy tắc phép trừ và hình bình hành ta có:

\(\begin{array}{l}\overrightarrow {B'B}  + \overrightarrow {CC'}  + \overrightarrow {D'D}  = \left( {\overrightarrow {AB}  - \overrightarrow {AB'} } \right) + \left( {\overrightarrow {AC'}  - \overrightarrow {AC} } \right) + \left( {\overrightarrow {AD}  - \overrightarrow {AD'} } \right)\\ = \left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right) - \overrightarrow {AC}  - \left( {\overrightarrow {AB'}  + \overrightarrow {AD'} } \right) + \overrightarrow {AC'} \\ = \overrightarrow {AC}  - \overrightarrow {AC}  - \overrightarrow {AC'}  + \overrightarrow {AC'}  = \overrightarrow 0 \,\,\left( 2 \right)\end{array}\)

Từ (1) và (2) ta có \(\overrightarrow {GB'}  + \overrightarrow {GC}  + \overrightarrow {GD'}  = \overrightarrow 0 \)  hay \(G\) cũng là trọng tâm tam giác \(B'CD'\).