Câu hỏi
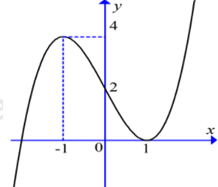
Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên trục trên \(\mathbb{R}\) và đồ thị hàm số \(y={f}'\left( x \right)\) như hình vẽ:
Số điểm cực trị của hàm số \(y=f\left( x \right)-5x\) là
- A 4
- B 3
- C 1
- D 2
Phương pháp giải:
Tính đạo hàm của hàm số \({g}'\left( x \right),\) xác định nghiệm của phương trình \(g\left( x \right)=0\) thông qua đồ thị hàm số \({f}'\left( x \right)\) suy ra số điểm cực trị của hàm số \(y=g\left( x \right)\)
Lời giải chi tiết:
Ta có \(g\left( x \right)=f\left( x \right)-5x\Rightarrow {g}'\left( x \right)={f}'\left( x \right)-5;\,\,\forall x\in \mathbb{R}.\) Phương trình \({g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)=5\,\,\,\,\,\,\,\,\,\,\left( * \right).\)
Dựa vào đồ thị hàm số \(y={f}'\left( x \right),\) ta thấy \(\left( * \right)\) có nghiệm duy nhất.
Vậy hàm số \(y=f\left( x \right)-5x\) có duy nhất 1 điểm cực trị.
Chọn C