Phương pháp giải:

Sử dụng phương pháp trừ thể tích để xác định thể tích của H.

Lời giải chi tiết:

Thể tích của hình chóp tứ giác đều là $V=\frac{1}{3}Sh=\frac{2}{3}.$

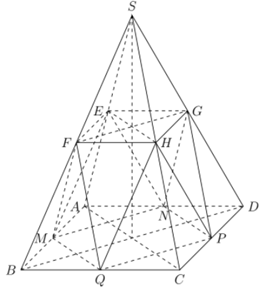
Gọi $M,\,\,N,\,\,P,\,\,\,Q,\,\,E,\,\,F,\,\,G,\,\,H$ là trung điểm tất cả các cạnh (hình vẽ).

Khi đó ${{V}_{MNPQ.EFGH}}={{V}_{S.ABCD}}-\left( {{V}_{S.EFGH}}+{{V}_{F.MBQ}}+{{V}_{H.QCP}}+{{V}_{G.PDN}}+{{V}_{E.MAN}} \right)$

Với ${{V}_{S.EFGH}}=\frac{1}{3}.\frac{1}{4}.1=\frac{1}{12}$ và các khối chóp còn lại cùng chiều cao, diện tích đáy bằng nhau nên thể tích ${{V}_{E.MAN}}=\frac{1}{3}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.1=\frac{1}{24}.$

Vậy thể tích cần tính là ${{V}_{MNPQ.EFGH}}=\frac{2}{3}-\frac{1}{12}=\frac{5}{12}.$

Chọn D