Câu hỏi
Cho \(\Delta ABC\) có trọng tâm \(G,\,\,H\) là điểm đối xứng của \(B\) qua \(G.\)
1. Chứng minh rằng \(\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} ,\,\,\,\overrightarrow {CH} = - \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\)
2. Gọi \(M\) là trung điểm của \(BC.\) CMR: \(\overrightarrow {MH} = \frac{1}{6}\overrightarrow {AC} - \frac{5}{6}\overrightarrow {AB} .\)
Lời giải chi tiết:
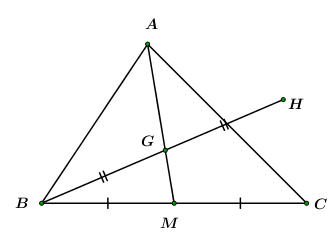
1. Ta có: \(\overrightarrow {AH} + \overrightarrow {AB} = 2\overrightarrow {AG} \) (quy tắc cộng hình bình hành)
Lại có: \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\)
\(\begin{array}{l} \Rightarrow \overrightarrow {AH} + \overrightarrow {AB} = 2\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\\ \Leftrightarrow \overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} .\end{array}\)
Tương tự ta có: \(\overrightarrow {CH} = \frac{2}{3}\overrightarrow {CA} - \frac{1}{3}\overrightarrow {CB} = \frac{2}{3}\overrightarrow {CA} - \frac{1}{3}\left( {\overrightarrow {CA} + \overrightarrow {AB} } \right) = \frac{1}{3}\overrightarrow {CA} - \frac{1}{3}\overrightarrow {AB} = - \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\)
2. Ta có: \(\overrightarrow {MH} = \overrightarrow {MC} + \overrightarrow {CH} = \frac{1}{2}\overrightarrow {BC} + \overrightarrow {CH} = \frac{1}{2}\overrightarrow {BA} + \frac{1}{2}\overrightarrow {AC} - \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\,\, = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} .\)
Vậy \(\overrightarrow {MH} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} .\)







