Câu hỏi
Đồ thị sau đây là của hàm số nào ?
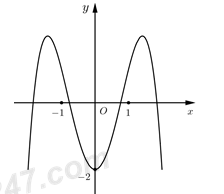
- A
\(y=-\,{{x}^{4}}+4{{x}^{2}}-2.\)
- B
\(y=-\,{{x}^{4}}+{{x}^{2}}-2.\)
- C
\(y={{x}^{4}}-{{x}^{2}}-2.\)
- D \(y={{x}^{4}}-{{x}^{2}}+2.\)
Phương pháp giải:
Dựa vào tính chất của đồ thị hàm số trùng phương
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy rằng :
Hàm số là hàm số trùng phương, có dạng \(y=a{{x}^{4}}+b{{x}^{2}}+c.\) Giới hạn \(\underset{x\,\to \,+\,\infty }{\mathop{\lim }}\,y=\underset{x\,\to \,-\infty }{\mathop{\lim }}\,y=-\,\infty \) \(\Rightarrow \) Hệ số \(a<0.\) Đồ thị hàm số cắt trục \(Oy\) tại \(\left( 0;-\,2 \right)\)\(\Rightarrow \) \(c=-\,2.\) Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt. Hàm số có ba điểm cực trị, trong đó có điểm cực trị có hoành độ lớn hơn 1.Vậy hàm số cần tìm là \(y=-\,{{x}^{4}}+4{{x}^{2}}-2.\)
Chọn A
Câu hỏi trước
