Câu hỏi
Một vật dao động điều hoà dọc theo một đường thẳng. Một điểm M nằm cố định trên đường thẳng đó, phía ngoài khoảng chuyển động của vật. Tại thời điểm t thì vật xa M nhất, sau đó một khoảng thời gian ngắn nhất là ∆t vật gần M nhất. Độ lớn vận tốc của vật bằng nửa tốc độ cực đại vào thời điểm gần nhất là
- A \(t + \frac{{2\Delta t}}{3}\)
- B \(t + \frac{{\Delta t}}{4}\)
- C \(t + \frac{{\Delta t}}{3}\)
- D \(t + \frac{{\Delta t}}{6}\)
Phương pháp giải:
Phương pháp: Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Đáp án D
Cách giải:
Tại thời điểm t vật xa M nhất => M ở biên âm
Tại thời điểm t + ∆t => M ở biên dương
=> ∆t = T/2 => T = 2∆t
Tại thời điểm t: vật ở vị trí biên thì vận tốc = 0
Tại thời điểm t + ∆t: độ lớn vận tốc của vật bằng nửa tốc độ cực. Biểu diễn trên đường tròn lượng giác của vận tốc ta có:
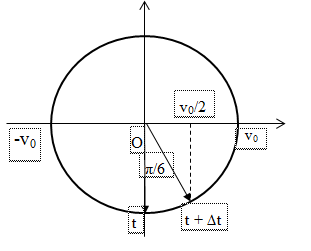
=> Góc quét α = π/6 => ∆t = (π/6).(T/2π) = T/12 = ∆t/6
=> Độ lớn vận tốc của vật bằng nửa tốc độ cực đại vào thời điểm: t + ∆t/6







