Phương pháp giải:

+)  \(SH\cap \left( ABCD \right)=C\Rightarrow \frac{d\left( H;\left( ABCD \right) \right)}{d\left( S;\left( ABCD \right) \right)}=\frac{HC}{SC}\)

+) Tính \({{V}_{H.ABCD}}=\frac{1}{3}d\left( H;\left( ABCD \right) \right).{{S}_{ABCD}}\)

Lời giải chi tiết:

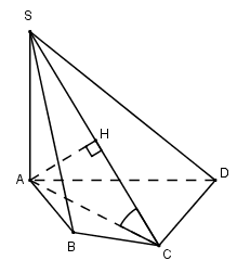
\(SA\bot \left( ABCD \right)\Rightarrow \) AC là hình chiếu vuông góc của SC trên (ABCD) \(\Rightarrow \widehat{\left( SC;\left( ABCD \right) \right)}=\widehat{\left( SC;AC \right)}=\widehat{SCA}={{60}^{0}}\)

Xét tam giác vuông SAC có: \(SC=\frac{AC}{\cos {{60}^{0}}}=\frac{a\sqrt{2}}{\frac{1}{2}}=2a\sqrt{2}\)

Xét tam giác vuông AHC có: \(HC=AC.\cos {{60}^{0}}=\frac{a\sqrt{2}}{2}\)

Ta có: \(SH\cap \left( ABCD \right)=C\Rightarrow \frac{d\left( H;\left( ABCD \right) \right)}{d\left( S;\left( ABCD \right) \right)}=\frac{HC}{SC}=\frac{\frac{a\sqrt{2}}{2}}{2a\sqrt{2}}=\frac{1}{4}\)

\(\Rightarrow d\left( H;\left( ABCD \right) \right)=\frac{1}{4}d\left( A;\left( ABCD \right) \right)=\frac{1}{4}SA=\frac{1}{4}AC.\tan {{60}^{0}}=\frac{1}{4}a\sqrt{2}.\sqrt{3}=\frac{a\sqrt{6}}{4}\)

Vậy \({{V}_{H.ABCD}}=\frac{1}{3}d\left( H;\left( ABCD \right) \right).{{S}_{ABCD}}=\frac{1}{3}.\frac{a\sqrt{6}}{4}.\frac{3{{a}^{2}}}{2}=\frac{{{a}^{3}}\sqrt{6}}{8}\)

Chọn C.