Phương pháp giải:

+) Xác định chiều cao của lăng trụ dựa vào dữ kiện \({A}'A={A}'B={A}'C=a\)

+) Sử dụng công thức tính diện tích tam giác đều cạnh \(a\) là \(S=\frac{{{a}^{2}}\sqrt{3}}{4}\)

+) Sử dụng công thức tính thể tích lăng trụ \(V=h.S\) với \(h,S\)lần lượt là chiều cao và diện tích đáy của lăng trụ

Lời giải chi tiết:

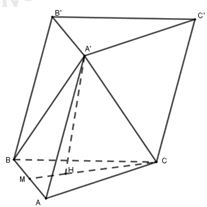
Gọi \(H\)là trọng tâm tam giác \(ABC\). Vì \({A}'A={A}'B={A}'C=a\) nên \({A}'H\bot \left( ABC \right)\).

Gọi \(M\) là trung điểm cạnh \(AB\).

Vì tam giác \(ABC\) đều cạnh \(a\) nên đường trung tuyến \(CM=\frac{a.\sqrt{3}}{2}\)

Suy ra \(CH=\frac{2}{3}CM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\).

Xét tam giác \({A}'HC\) vuông tại \(H\) ta có \({A}'H=\sqrt{{A}'{{C}^{2}}-C{{H}^{2}}}=\sqrt{{{a}^{2}}-\frac{{{a}^{2}}}{3}}=\frac{\sqrt{6}}{3}a\)

Diện tích tam giác đều \(ABC\) là \({{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}\).

Ta có \({{V}_{ABC.{A}'{B}'{C}'}}={A}'H.{{S}_{ABC}}=\frac{a\sqrt{6}.{{a}^{2}}\sqrt{3}}{3.4}=\frac{{{a}^{3}\sqrt{2}}}{4}\).

Chọn B.