Câu hỏi
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ.
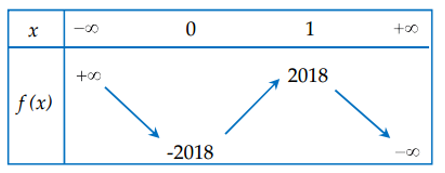
Hỏi phương trình \(\left| f\left( x+2017 \right)-2018 \right|=2019\) có bao nhiêu nghiệm?
- A \(6\).
- B \(2\).
- C \(4\).
- D \(3\).
Phương pháp giải:
Sử dụng các phép tịnh tiến đồ thị hàm số (lên trên, xuống dưới, sang phải, sang trái)
Sau đó lập BBT của đồ thị hàm số chứa giá trị tuyệt đối
Dựa vào sự tương giao của hai đồ thị hàm số để kết luận số nghiệm của phương trình đã cho.
Lời giải chi tiết:
Từ đồ thị hàm số \(y=f\left( x \right)\)ta tịnh tiến xuống dưới \(2018\) đơn vị ta được đồ thị hàm số \(y=f\left( x \right)-2018\).
Từ đó ta có BBT của hàm số \(y=f\left( x \right)-2018\) là
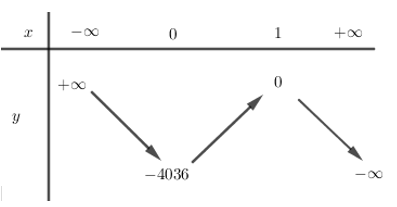
Lại suy ra BBT của hàm số \(y=\left| f\left( x \right)-2018 \right|\) là
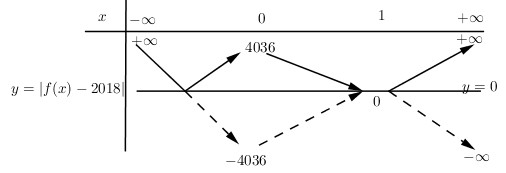
Nhận thấy khi ta tịnh tiến đồ thị hàm số \(y=\left| f\left( x \right)-2018 \right|\) theo vec tơ \(\overrightarrow{u}\left( 2017;0 \right)\) (sang phải 2017 đơn vị) thì ta được đồ thị hàm số \(y=\left| f\left( x+2017 \right)-2018 \right|\)
Nhận thấy rằng số giao điểm của đồ thị hàm số \(y=\left| f\left( x+2017 \right)-2018 \right|\) và đường thẳng \(y=2019\) bằng với số giao điểm của đồ thị hàm số \(y=\left| f\left( x \right)-2018 \right|\) và đường thẳng \(y=2019\) và cũng chính là số nghiệm của phương trình \(\left| f\left( x+2017 \right)-2018 \right|=2019\)
Từ BBt của \(y=\left| f\left( x \right)-2018 \right|\) ta thấy đường thẳng \(y=2019\) cắt đồ thị hàm số \(y=\left| f\left( x \right)-2018 \right|\) tại
bốn điểm phân biệt nên phương trình \(\left| f\left( x+2017 \right)-2018 \right|=2019\) có bốn nghiệm phân biệt.
Chọn C.







