Phương pháp giải:

\({{x}_{0}}\) là điểm cực đại của hàm số thì \({f}'\left( {{x}_{0}} \right)=0\) và \({f}'\left( x \right)\) đổi dấu từ dương sang âm tại \({{x}_{0}}\).

Lời giải chi tiết:

Ta có \(f'\left( x \right) = \left( {x - 1} \right)\left( {3 - x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)

Bảng xét dấu của

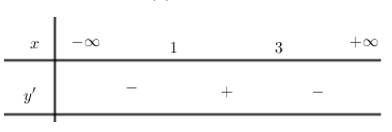
Từ bảng xét dấu ta có \(x=3\) là điểm cực đại của hàm số \(y=f\left( x \right)\)

Chọn C.