Câu hỏi
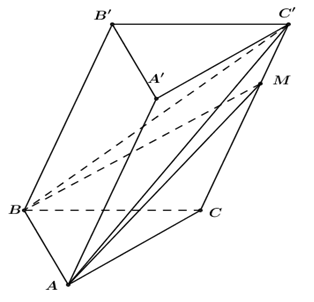
Cho hình lăng trụ ABC.A’B’C’ có thể tích là V. Gọi M là điểm thuộc cạnh CC’ sao cho \(CM=2C'M.\) Tính thể tích của khối chóp MABC.
- A \(\frac{2V}{3}\)
- B \(\frac{V}{3}\)
- C \(\frac{V}{9}\)
- D \(\frac{2V}{9}\)
Phương pháp giải:
+) Sử dụng định tỉ số thể tích để tính.
Lời giải chi tiết:
Ta có: \(\frac{{{V}_{MABC}}}{{{V}_{C'ABC}}}=\frac{MC}{C'C}=\frac{2}{3}\Rightarrow {{V}_{MABC}}=\frac{2}{3}{{V}_{C'ABC}}.\)
Lại có \({{V}_{C'ABC}}=\frac{1}{3}{{V}_{ABC.A'B'C'}}=\frac{1}{3}V.\)
\(\Rightarrow {{V}_{MABC}}=\frac{2}{3}{{V}_{C'ABC}}=\frac{2}{3}.\frac{1}{3}V=\frac{2}{9}V.\)
Chọn D.
Câu hỏi trước
