Câu hỏi
Đường cong trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
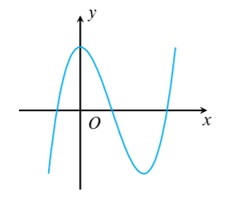
- A \(y=-{{x}^{3}}+3{{x}^{2}}+2\).
- B \(y={{x}^{3}}-3x+2\).
- C \(y=-{{x}^{4}}+2{{x}^{2}}-2\).
- D \(y={{x}^{3}}-3{{x}^{2}}+2\).
Phương pháp giải:
- Quan sát dáng đồ thị để nhận dạng đồ thị, tìm các điểm cực trị của đồ thị hàm số và rút ra kết luận.
Lời giải chi tiết:
Quan sát đồ thị hàm số, ta thấy:
+ Đây không phải là đồ thị của hàm số bậc bốn trùng phương \(\Rightarrow \)Loại phương án C.
Còn lại phương án A, B, D đều là các hàm số bậc ba
(dạng \(y=a\,{{x}^{3}}+b{{x}^{2}}+cx+d,\,\,a\ne 0\))
+) Khi \(x\to +\infty \) thì \(y\to +\infty \Rightarrow a>0\): Loại phương án A.
+ Hàm số đạt cực trị tại x = 0 , ta loại phương án B vì \(y'=3{{x}^{2}}-3\) không nhận \(x=0\) là nghiệm.
Ta chọn phương án D.
Chọn: D.







