Phương pháp giải:

+) Lập bảng biến thiên của đồ thị hàm số \(f\left( x \right)=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m\).

+) Từ BBT của đồ thị hàm số \(f\left( x \right)=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m\) suy ra BBT của đồ thị hàm số \(y=\left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m \right|\)

+) Dựa vào đồ thị của hàm số \(y=\left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m \right|\), tìm điều kiện để nó có 7 cực trị.

Lời giải chi tiết:

Xét hàm số \(y=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m\) có \(y'=12{{x}^{3}}-12{{x}^{2}}-24x=0\Leftrightarrow 12x\left( {{x}^{2}}-x-2 \right)=0\Leftrightarrow \left[ \begin{align}  & x=0 \\  & x=-1 \\  & x=2 \\ \end{align} \right.\)

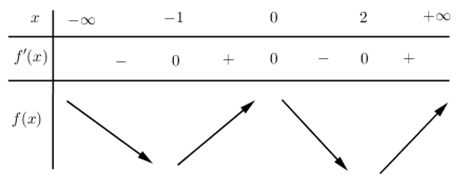
Lập BBT của đồ thị hàm số \(f\left( x \right)=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m\) ta có :

Đồ thị hàm số \(y=\left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m \right|\) được vẽ bằng cách :

+) Lấy đối xúng phần đồ thị hàm số nằm phía dưới trục Ox qua trục Ox.

+) Xóa đi phần đồ thị bên dưới trục Ox.

Do đó để đồ thị hàm số \(y=\left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m \right|\) có 7 điểm cực trị thì :

\(\begin{array}{l}
\left\{ \begin{array}{l}
f\left( 0 \right) > 0\\
f\left( { - 1} \right) < 0\\
f\left( 2 \right) < 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m > 0\\
- 5 + m < 0\\
- 32 + m < 0
\end{array} \right. \Leftrightarrow 0 < m < 5\\
m \in Z \Rightarrow m \in \left\{ {1;2;3;4} \right\}
\end{array}\)

Vậy có 4 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Chọn D.