Câu hỏi
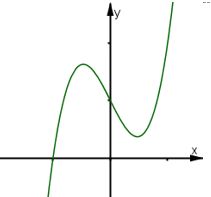
Hàm số \(y=f\left( x \right)\) có đồ thị \(y=f'\left( x \right)\) như hình vẽ. Khi đó số điểm cực trị của hàm số \(y=f\left( x \right)\) là:
- A 2
- B 1
- C 3
- D 4
Phương pháp giải:
+) Quan sát đồ thị hàm số, nhận xét tính chất của hàm số \(y=f'\left( x \right)\). Từ đó suy ra số điểm cực trị của hàm số \(y=f\left( x \right).\)
+) Hàm số đạt cực trị tại \(x={{x}_{0}}\Leftrightarrow y'\left( {{x}_{0}} \right)=0.\)
Lời giải chi tiết:
Ta thấy đồ thị hàm số \(y=f'\left( x \right)\) cắt trục hoành tại 1 điểm duy nhất hay phương trình \(y'=0\) có 1 nghiệm duy nhất.
Vậy hàm số \(y=f\left( x \right)\) có 1 điểm cực trị.
Chọn B.