Câu hỏi
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD = 2a, AA’ = 3a nội tiếp mặt cầu (S). Tính diện tích mặt cầu (S).
- A \(6\pi {{a}^{2}}.\)
- B \(56\pi {{a}^{2}}.\)
- C \(14\pi {{a}^{2}}.\)
- D \(\frac{7\pi {{a}^{2}}}{2}.\)
Lời giải chi tiết:
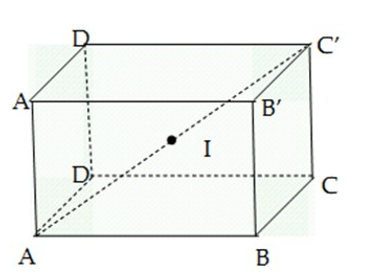
Gọi I là tâm của hình hộp chữ nhật ABCD.A’B’C’D’.
Bán kính mặt cầu (S) : \(R=\frac{AC'}{2}=\frac{\sqrt{A{{B}^{2}}+A{{D}^{2}}+AA{{'}^{2}}}}{2}=\frac{\sqrt{{{a}^{2}}+{{(2a)}^{2}}+{{(3a)}^{2}}}}{2}=\frac{\sqrt{14}a}{2}\)
Diện tích mặt cầu (S): \({{S}_{mc}}=4\pi {{R}^{2}}=4.\pi .\left( \frac{\sqrt{14}a}{2} \right)=14\pi {{a}^{2}}\)
Chọn: C.
Câu hỏi trước
