Phương pháp giải:

- Sử dụng tính chất đối xứng của tâm đối xứng của hàm số bậc 3.

Lời giải chi tiết:

\(\begin{array}{l}y = {x^3} - 3{x^2} \Rightarrow y' = 3{x^2} - 6x \Rightarrow y'' = 6x - 6\\y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\\y'' = 0 \Leftrightarrow x = 1\end{array}\)

Đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}\)(C) có điểm cực đại \(A(0;0)\), điểm cực tiểu \(B(2;-4)\) và tâm đối xứng \(I(1;-2)\).

Để (C) cắt đường thẳng y = m tại 3 điểm phân biệt thì

-4 < m < 0.

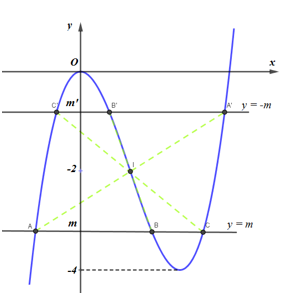
Giả sử tồn tại số \(m\in (-4;0)\)thỏa mãn yêu cầu của đề bài, (C) cắt đường thẳng y = m tại 3 điểm phân biệt A, B, C.

Do (C) có tâm đối xứng là \(I(1;-2)\)nên ta xác định được các điểm A’, B’, C’ nằm trên (C) lần lượt là điểm đối xứng của A, B, C qua I.

Dễ dàng chứng minh được, A’ B’, C’ cũng thỏa mãn : A’B’ = 2 B’C’ và ta có \(\frac{m+m'}{2}=-2\Rightarrow m+m'=-4\)

Ta thấy, tồn tại duy nhất 2 số m thỏa mãn đề bài.

Vậy, tổng các phần tử thuộc S là – 4 .

Chọn: B.