Câu hỏi
Cho nửa đường tròn tâm O, đường kính AB. Người ta ghép hai bán kính OA, OB lại tạo thành mặt xung quanh một hình nón. Tính góc ở đỉnh của hình nón đó.
- A \({{30}^{0}}.\)
- B \({{45}^{0}}.\)
- C \({{60}^{0}}.\)
- D \({{90}^{0}}.\)
Lời giải chi tiết:
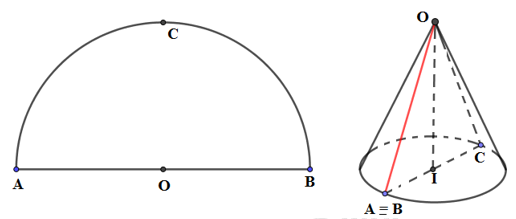
Gọi C là điểm chính giữa cung AB, khi ghép 2 bán kính OA, OB tạo thành hình nón, điểm A trùng B và AC (BC) là đường kính của đường tròn đáy.
\(\Rightarrow \)Góc ở đỉnh của hình nón là \(\widehat{AOC}\).
Gọi \({{C}_{1}}\) là chu vi đường tròn bán kinh OA, \({{C}_{2}}\)là chu vi đường tròn bán kính IA.
Theo đề bài, ta có: \({{C}_{1}}=2{{C}_{2}}\Leftrightarrow 2\pi .OA=2.2\pi .IA\Rightarrow OA=2.IA\Rightarrow OA=AC\).
\(\Rightarrow \Delta OAC\)đều.
\(\Rightarrow \widehat{AOC}={{60}^{0}}.\)
Chọn: C.
Câu hỏi trước
