Lời giải chi tiết:

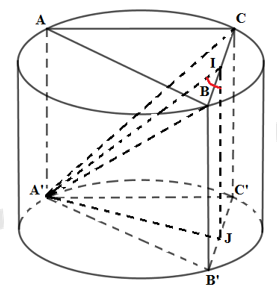
Gọi I, J lần lượt là trung điểm BC, B’C’.

Ta có góc giữa hai mặt phẳng \((A'BC)\)và .\((ABC)\).là góc \(\widehat{AIA'}\)bằng \({{45}^{0}}\).

Ta có:

\(\begin{array}{l}\frac{{{S_{A'B'C'}}}}{{{S_{A'BC}}}} = \frac{{\frac{1}{2}A'J.B'C'}}{{\frac{1}{2}A'I.BC}} = \frac{{A'J}}{{A'I}} = \sin \widehat {JIA'} = \sin \widehat {AIA'} = \sin {45^0} = \frac{1}{{\sqrt 2 }}\\ \Rightarrow {S_{A'B'C'}} = \frac{{{S_{A'BC}}}}{{\sqrt 2 }} = \frac{{{a^2}\sqrt 6 }}{{\sqrt 2 }} = {a^2}\sqrt 3 \end{array}\)

Tam giác A’B’C’ đều, suy ra: \({{S}_{A'B'C'}}=\frac{A'B{{'}^{2}}\sqrt{3}}{4}={{a}^{2}}\sqrt{3}\Rightarrow A'B'=2a\Rightarrow A'J=2a.\frac{\sqrt{3}}{2}=a\sqrt{3}\)

Lại có \(\Delta A'IJ\)  vuông cân tại J (do \(A'J\bot IJ\) ) :

\(\Rightarrow l=IJ=A'J=a\sqrt{3}\), (\(l\): độ dài đường sinh của hình trụ).

    \(R=\frac{2}{3}A'J=\frac{2}{3}a\sqrt{3}=\frac{2a\sqrt{3}}{3}\) (\(R\): bán kính đường tròn ngoại tiếp đáy, đáy là tam giác đều).

Diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ \(ABC.ABC\):

                              \({{S}_{xq}}=2\pi Rl=2\pi .\frac{2a\sqrt{3}}{3}.a\sqrt{3}=4{{a}^{2}}\pi \)

Chọn C.