Câu hỏi
Cho hình trụ có bán kính r = 5cm và chiều cao \(h=5\sqrt{3}cm\). Cắt hình trụ bởi một mặt phẳng song song và cách trục 3cm ta được một thiết diện. Tính diện tích thiết diện đó.
- A \(100\sqrt{3}c{{m}^{2}}\)
- B \(20\sqrt{3}c{{m}^{2}}\)
- C \(40\sqrt{3}c{{m}^{2}}\)
- D \(80\sqrt{3}c{{m}^{2}}\)
Phương pháp giải:
Thiết diện của hình trụ cắt bởi một mặt phẳng song song với trục là hình chữ nhật.
Lời giải chi tiết:
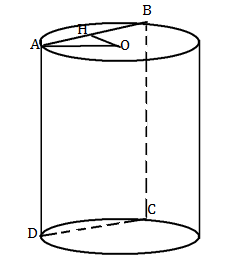
Gọi ABCD là thiết diện, H là trung điểm của AB ta có \(OH\bot \left( ABCD \right)\Rightarrow OH=3\,\left( cm \right)\)
Xét tam giác vuông OHA có
\(AH=\sqrt{O{{A}^{2}}-O{{H}^{2}}}=\sqrt{{{5}^{2}}-{{3}^{2}}}=4\Rightarrow AB=2AH=8\)
\(AD=h=5\sqrt{3}\left( cm \right)\Rightarrow {{S}_{ABCD}}=AB.AD=8.5\sqrt{3}=40\sqrt{3}c{{m}^{2}}\)
Chọn C
Câu hỏi trước
